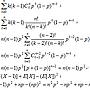Re: [教學] 二項分布標準差的教法請益
可以利用
Var(X) = E(X^2) - E(X)^2
= E(X^2)-E(X)+E(X)- E(X)^2
=E[X(X-1)]+E[X]-E(X)^2
http://imgur.com/FaCimBw

※ 引述《kyoiku (生死間有大恐怖)》之銘言:
: 我直接證明,學生全倒......
: 想請教大家有沒有比較直觀的方法或簡易的證明,ORZ
: 我這樣證:
: 由 Var(X) = E(X^2) - E(X)^2
: = E(X^2) - (np)^2
: 所以只要算出 E(X^2) 代入整理就好了
: 由期望值定義 =>
: E(X^2) = sigma(k from 0 to n) (k^2)P(X=k)
: 下去展開、約分、提出np、變數變換等等算出再代回,
: 學生真的沒這麼厲害,QQ
: 想請教大家這邊是怎麼教的,謝謝
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 111.243.90.123
※ 文章網址: https://www.ptt.cc/bbs/tutor/M.1432132609.A.B73.html
推
05/20 23:50, , 1F
05/20 23:50, 1F
→
05/20 23:59, , 2F
05/20 23:59, 2F
→
05/21 00:00, , 3F
05/21 00:00, 3F
推
05/25 23:22, , 4F
05/25 23:22, 4F
討論串 (同標題文章)
tutor 近期熱門文章
PTT職涯區 即時熱門文章