Re: [解題] 國三相似形

看板tutor (家教)作者gwendless (望月‧老蔣)時間11年前 (2014/10/03 13:41)推噓1(1推 0噓 0→)

留言1則, 1人參與討論串3/3 (看更多)

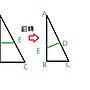
※ 引述《ShockIdle (新的開始)》之銘言： : 題目：http://ppt.cc/T42x : 想法：做輔助圓，BCDE四點共圓而使得三角形ADE~三角形ACB : 但目前國三學生還沒學到圓 : 不知道有沒有其他方法可以解 : 謝謝指教思路是這樣的條件給的是面積比，而要我們去求長度所以聯想到可能是 (面積比) = (對應邊長平方比) 的性質但是ADE與BCDE的分割看不出任何相似形關係不過解題經驗告訴我們，有一種相似三角形的題型，有類似的味道 http://imgur.com/lBnjOzD

所以猜測 ΔADE ~ ΔACB 題目沒什麼長度的條件，所以從AA相似去著手假設一開始的∠ADE=α、∠AED=β，由此可直觀推出∠CDE=90-α、∠BED=90-β 接著，觀察四邊形BCDE內中的四個三角形，其實是兩兩相似的證明不難，分別用AA及SAS即可解決。故省略所以按對應角關係，∠EBC = ∠CDE = 90-α、∠DCB = ∠BED=90-β 再由ΔBCD、ΔECB的內角和關係推出 ∠ABC=β、∠ACB=α 至此，AA性質成立，ΔADE ~ ΔACB得證接著是長度的問題由翻轉過後的圖形的 (面積比)=(對應邊長平方比) 關係 __ 可推出 AE = 18/5 __ 輔以已知的 AB = 6 、以及，翻轉前的ΔAEB是個直角三角形 __ 所以畢氏定理求得 BE = 24/5 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 220.136.88.206 ※ 文章網址: http://www.ptt.cc/bbs/tutor/M.1412314906.A.000.html ※ 編輯: gwendless (220.136.88.206), 10/03/2014 13:46:59